


Different numbers of arcs indicate different angles.The same number of arcs indicate equal angles.Different numbers of hash marks indicate different lengths.The same number of hashes indicate equal lengths.To classify a triangle using comparative lengths or angles: Recognise that arcs in vertices can be used to indicate equal angles.Recognise that hash marks indicate equal lengths.Thus, when two triangles are congruent then according to CPCTC the other corresponding side and the other two corresponding angles are also equal. In other words, the two triangles are said to be congruent if two corresponding sides and the included angle are equal. In SAS triangle congruence the two corresponding sides and the included angle are equal. How do you Prove CPCTC Using SAS Criterion? Thus, when two triangles are congruent then according to CPCTC all the corresponding angles are also equal. In other words, the two triangles are said to be congruent if all corresponding sides of one triangle are equal to the sides of another triangle. In SSS triangle congruence all the three corresponding sides are equal. How do you Prove CPCTC Using SSS Criterion? For example, triangle ABC and triangle PQR are congruent triangles therefore according to the theorem the sides AB = PQ, BC = QR, and CA = RP.
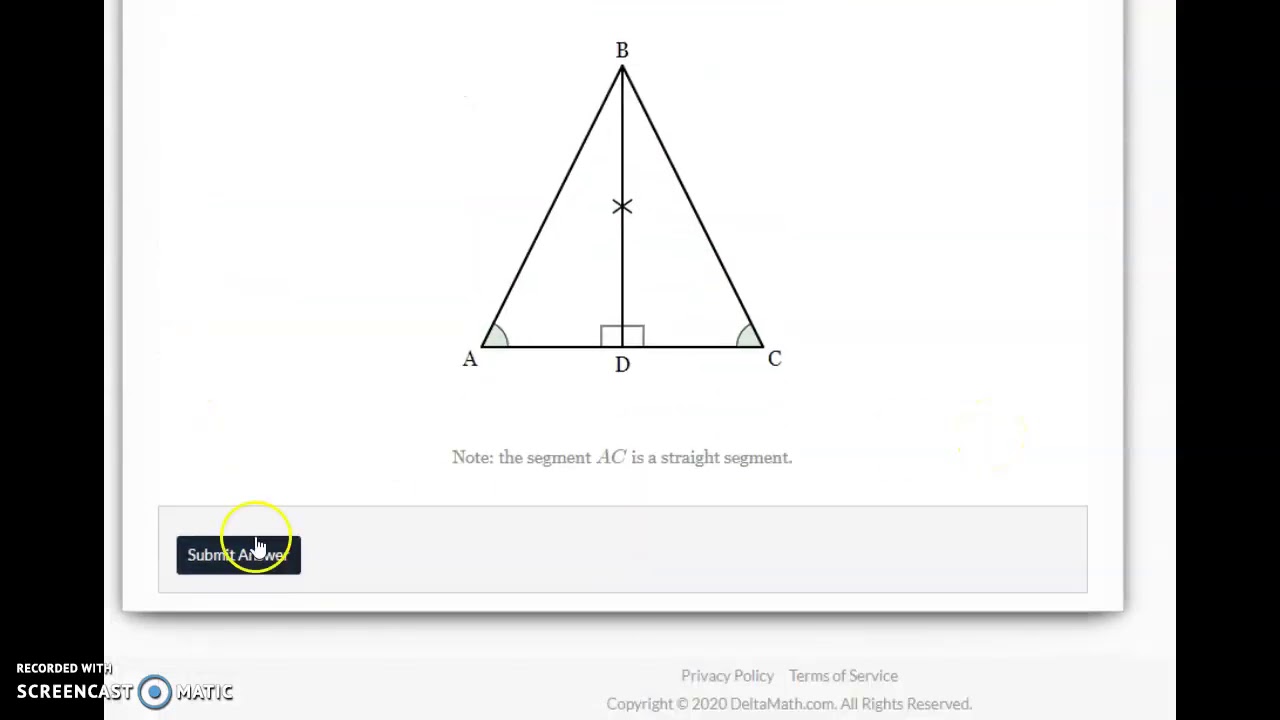
The theorem CPCTC tells that when two triangles are congruent then their corresponding sides and angles are also said to be congruent. Sometimes, it is also called CPCT which means corresponding parts of congruent triangles. What does CPCTC Stand for?ĬPCTC stands for corresponding parts of congruent triangles are congruent. It can be justified by superimposing triangles on each other and then by observing the corresponding angles and side lengths. How do you Prove CPCTC?Īfter showing the proposed triangles are congruent, we can immediately say that the corresponding parts of congruent triangles are congruent. Corresponding angles of the two similar triangles are equal, whereas, corresponding sides of the triangles are not equal, but proportional. So, we cannot apply the CPCTC theorem for similar triangles. What is CPCTC for Similar Triangles?ĬPCTC for similar triangles is not true. Corresponding means angles and sides that are in the same respective position in the two triangles. CPCTC is a theorem that says corresponding parts of congruent triangles are congruent. AB = LM, BC = MN, AC = LN, and ∠ A = ∠L, ∠B = ∠M, ∠C = ∠N. And if △ABC ≅ △LMN, then as per the CPCTC theorem, the corresponding sides and angles are equal, i.e. ∠A corresponds to ∠L, ∠B corresponds to ∠M, ∠C corresponds to ∠N. AB corresponds to LM, BC corresponds to MN, AC corresponds to LN. the three corresponding sides and the three corresponding angles. In these two triangles ABC and LMN, let us identify the 6 parts: i.e. It means that the three pairs of sides and three pairs of angles of △ABC are equal to the three pairs of corresponding sides and three pairs of corresponding angles of △LMN. Corresponding angles mean the three angles in one triangle are in the same position or spot as in the other triangle.
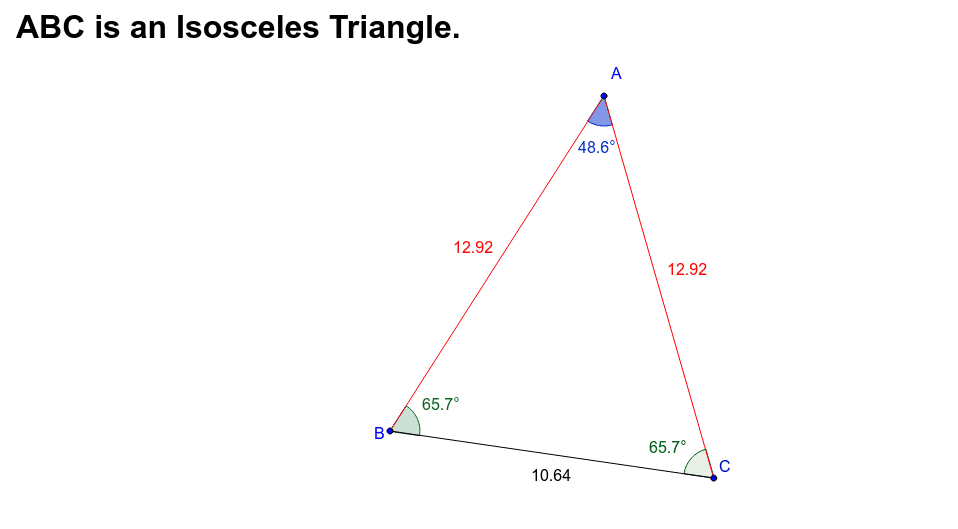
Two congruent triangles have three equal sides and equal angles with respect to each other.Ĭorresponding sides mean the three sides in one triangle are in the same position or spot as in the other triangle. Two triangles are said to be congruent if they have exactly the same size and the same shape. Let us understand the meaning of congruent triangles and corresponding parts in detail. This means, when two or more triangles are congruent then their corresponding sides and angles are also congruent or equal in measurements. The CPCTC theorem states that when two triangles are congruent, then every corresponding part of one triangle is congruent to the other. The abbreviation CPCTC is for Corresponding Parts of Congruent Triangles are Congruent.


 0 kommentar(er)
0 kommentar(er)
